Eleição do(a) líder do Projeto Debian 2020

Linha do tempo

Período de candidatura: Domingo, 8 de março de 2020 00:00:00 UTC Sábado, 14 de março de 2020 23:59:59 UTC
Período de campanha: Domingo, 15 de março de 2020 00:00:00 UTC Sábado, 4 de abril de 2020 23:59:59 UTC
Período de votação: Domingo, 5 de abril de 2020 00:00:00 UTC Sábado, 18 de abril de 2020 23:59:59 UTC

Por favor observe que o novo mandato do(a) líder do projeto deve começar em 21 de abril de 2020.

Candidaturas

  1. Jonathan Carter [[email protected]] [e-mail de candidatura] [plataforma]
  2. Sruthi Chandran [[email protected]] [e-mail de candidatura] [plataforma]
  3. Brian Gupta [[email protected]] [e-mail de candidatura] [plataforma]

A cédula, quando estiver pronta, pode ser solicitada por e-mail, enviando uma mensagem assinada para [email protected] com o assunto leader2020.

Dados e estatísticas

Esse ano, como sempre, serão coletadas estatísticas sobre as cédulas recebidas e os reconhecimentos enviados periodicamente durante o período de votação. Além disso, a lista de eleitores(as) será registrada. E também, o registro de contagem estará disponível para visualização. Por favor lembre-se de que a eleição do(a) líder do projeto tem uma cédula secreta, portanto, o registro de contagem não conterá o nome do(a) eleitor(a), mas um HMAC (código de autenticação com base em hash) que permitirá aos(às) eleitores(as) verificar se seu voto está na lista de votos. Existe uma chave gerada para cada eleitor(a) que é enviada junto com a confirmação do voto

Quorum

Com a lista atual de desenvolvedores(as) votantes , temos 

 Número atual de desenvolvedores = 1011
 Q ( raíz quadrada (núm. desenvolvedores) / 2 ) = 15.8981130955846
 K min(5, Q )           = 5
 Quorum  (3 x Q )       = 47.6943392867539

Obs: Não usamos o formato "desenvolvedores(as)" para não gerar confusão com os parênteses da fórmula.

Quorum

Maioria requerida

Os(As) candidatos(as) precisam de maioria simples para serem elegíveis.

Maioria

Resultado

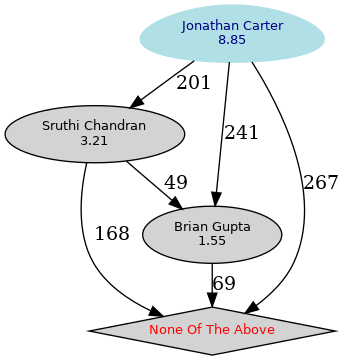
Representação gráfica dos resultados

No gráfico acima, quaisquer nós de cor rosa implicam que a opção não superou a maioria, o azul é o vencedor. O octógono é usado para as opções que não superaram o padrão.

Na tabela a seguir, o par[linha x][coluna y] representa os votos que a opção x recebeu sobre a opção y. Uma explicação mais detalhada da matriz de duelos pode ajudar na compreensão da tabela. Para entender o método de Condorcet, a página da Wikipedia é bastante informativa.

A matriz de duelos
 Opções
  1 2 3 4
Opção 1   258 281 301
Opção 2 57   163 244
Opção 3 40 114   194
Opção 4 34 76 125  

Olhando a linha 2, coluna 1, Sruthi Chandran
recebeu 57 votos sobre Jonathan Carter

Olhando a linha 1, coluna 2, Jonathan Carter
recebeu 258 votos sobre Sruthi Chandran.

Vitórias por pares

O conjunto de Schwartz contém

Os(As) vencedores(as)

O Debian usa o método de Condorcet para votação. De forma simplista, o método de Condorcet puro pode ser declarado da seguinte forma:
Considere todos os possíveis enfrentamentos entre pares de candidatos(as). O(A) vencedor(a) do Condorcet, se houver, é o(a) candidato(a) que vencer cada um dos(as) outros(as) candidatos(as) nesse enfrentamento por pares. O problema é que, em eleições complexas, pode muito bem haver uma relação circular em que A vence B, B vence C, e C vence A. A maioria das variações no Condorcet usa vários meios de resolver o empate. Veja Cloneproof Schwartz Sequential Dropping (o método Schulze) para mais detalhes. A variante do Debian é explicada na constituição, especificamente, A.6.

Secretário do projeto Debian